As youth development educators, we are always trying to find new ways to incorporate more “teachable moments” into our lessons to broaden the learning experience of our students. In addition, we are always trying to integrate science related activities (such as archery) back to S.T.E.M. This article does just that. It uses a common building construction technique, the 3-4-5- rule of making something square, and relates it back to the topic at hand, in this case archery, and then highlights the underlying mathematics principle. I’d like to thank Dr. Mike Lindstrom, a Minnesota educator and S.T.E.M. promoter for the technical explanation of the Pythagorean Theorem.
Construction projects often need to have precise 90 degree or “square” angles. But often the available tools (such as a carpenter’s square) are simply too small to guarantee the accuracy needed for large projects such as laying out the foundation of a house; therefore carpenters, concrete framers, (and archery instructors) will often employ a 3-4-5 triangle technique to ensure accurate 90 degree angles.
Using The Pythagorean Theorem In Theory
The technique simply requires that a person create a triangle in the corner of the lines that are to be square (90 degrees) to each other. The triangle must have one side (leg) that is 3 feet long, a second side that is 4 feet long and a third side that is 5 feet long. Any triangle with sides of 3, 4 and 5 feet will have a 90 degree angle opposite the 5 foot side. If a larger triangle is needed to increase accuracy of very large structures, any multiple of 3-4-5 could be used (such as a 6-8-10 foot triangle or a 9-12-15 foot triangle).
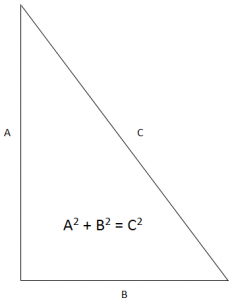 In Geometry, a well known method of constructing a right angle is to employ the Pythagorean Theorem. The mathematician, Pythagoras, discovered a relationship between the sides of any right triangle that is now known as the Pythagorean Theorem; he proved that the square of the longest side (the hypotenuse) is equal to the sum of the squares of the remaining two sides. This is often expressed as the following equation A2 + B2 = C2. (M. Lindstrom, 2007)
In Geometry, a well known method of constructing a right angle is to employ the Pythagorean Theorem. The mathematician, Pythagoras, discovered a relationship between the sides of any right triangle that is now known as the Pythagorean Theorem; he proved that the square of the longest side (the hypotenuse) is equal to the sum of the squares of the remaining two sides. This is often expressed as the following equation A2 + B2 = C2. (M. Lindstrom, 2007)
Using The Pythagorean Theorem In Practice
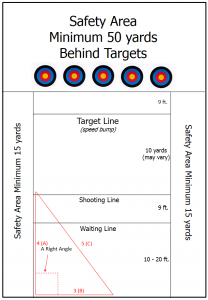
The purpose of this calculation is to layout a shooting range in a perfect right angle. A pre-marked 100-foot rope or 100 foot tape measure are tools for this purpose. Leg A is the yardage line marker, Leg B is the shooting line, and Leg is the hypotenuse. Ideally, Leg C would not exceed the overall length of the measuring tool. Use any one of the trio combinations below in laying out your range. Please note this word of caution, for large archery ranges not set up with this precision, it is easy to make it out of square by making simple measurements. That inaccuracy could result in giving one archer an advantage over another, if the targets are at differing distances from the shooting line.
Range Lay Out Using A Right Angle Calculation
|
Triangle Leg A |
Triangle Leg B |
Triangle Leg C |
|
3 (feet, yards or meters) |
4 |
5 |
|
6 |
8 | 10 |
|
9 |
12 |
15 |
|
12 |
16 |
20 |
|
15 |
20 |
25 |
Sources:
• Dr. Mike Lindstrom, Link to the original article.
• National 4-H Shooting Sports, Archery Instructor Manual, http://www.4-hshootingsports.org/
 0
0

Comments:
March 29, 2022
Hi Laura, Currently, we do not have any permaculture classes. Our horticulture agent, Sally, might have some information on it though. You can contact her at sasc@ufl.edu
March 27, 2022
Do you have classes regarding Perma Culture? My daughter-in-law was talking to me about this and I am hoping you have available information. Thanks
February 10, 2022
Hello, We have another pressure canning class coming up on March 5 from 10 am to 12 pm. You can find it on our Eventbrite page: https://www.eventbrite.com/o/ufifas-extension-brevard-county-18496539748
February 10, 2022
I was wondering if another pressure canning class is coming up? I missed the one this month unfortunately and am very interested in learning this skill!
November 17, 2021
Hi Dianna, I have a post scheduled to go out on 11/24. If you would like to receive our class list sooner, we have a newsletter that goes out on the 3rd Monday of every month! You can subscribe to it here: https://bit.ly/3CxvPY4
November 16, 2021
When will they post December classes?
October 12, 2021
Dear Dr. Wells, I admire your work to find the happy environmentally friendly balance of natural ecosystems within golf courses. We have found many supporters who wish to reinvent the abandoned , privately -owned West End golf course on Newberry Road in Alachua County, and are reaching out to our County government for their support as well. The golf course was the core of our West End Village neighborhood ; we have a dream to revitalize it. Looking forward to contacting you at a later time! Thank you.
October 11, 2021
Hi Laura, Thanks for your comment! I missed it earlier, I apologize. Please feel free to quote me and reach out if you have any questions. Several of our golf courses have become certified with Audubon International for their conservation efforts! I also have an article you may be interested in here, page 16: https://cdn.ymaws.com/www.ftga.org/resource/resmgr/turf_digest/2019/ftd_septoct_2019.pdf
October 11, 2021
This blog is very informative the stuff you provide I really enjoyed reading
October 9, 2021
Pls specify, as well, Bonnie, which of the plants in your table r native to Florida.
October 8, 2021
It’s truly a nice and helpful piece of information. I’m happy that you simply shared this helpful information with us. 바둑이사이트넷
September 29, 2021
You're welcome. Glad I could provide useful information. Thanks for reading.
September 20, 2021
This is actually the kind of information I have been trying to find. Thank you for writing this information about preschool playground equipment
September 5, 2021
I am a huge fan of Greenspaces/ Golf Courses. I love the statement you make underlining the importance of golfcourse superintendents as “stewards of the land. “May I please quote you ? I’m writing our commissioners to help save an abandoned for sale golf course! I love seeing deer, red tailed hawks, Sandhill Cranes on this former course. I’ve also seen a pair of pileated woodpeckers, a flock of egrets, and bluebirds.
August 23, 2021
Hello Michael, It's possible that the class in Cocoa is already full. Please contact the instructor, Gus Koerner, at (321) 633-1702 ext. 52320 or email him at gkoerner@ufl.edu for further information.
August 21, 2021
Hello! the Hunter Safety Class is NOT listed on the FWC class list.. My son needs the class, it has been canceled twice..he is signed up for the 3 hour virutal on AUG 24th, but if this cancels, we would like to do the 28th class in Cocoa.. Please advise! Thank YOU! Mike
August 19, 2021
I simply want to tell you that I am just beginner to blogs and really enjoyed you’re web page. Very likely I’m planning to bookmark your site . You really have fantastic posts. 토토
July 22, 2021
I've been looking for photos and articles on this topic over the past few days due to a school assignment, and I'm really happy to find a post with the material I was looking for! I bookmark and will come often! Thanks :D 먹튀신고
July 17, 2021
thanks for sharing best information
July 7, 2021
Hi Chris, Yes, these are "Florida-Friendly" plants, meaning they are low impact, environmentally friendly, use less water and reduce pollutant loading to Florida waters. Learn more here: https://ffl.ifas.ufl.edu/ Thanks! Bonnie
July 1, 2021
Hello, I just want to clarify... Under "Florida Friendly" cloumn, are you saying the plants do well in the Florida environment OR the plants are dangerous because of the ability to spread and damage the environment like Kudzu in Georgia? I live in Boca Raton, in Palm Beach County, which I believe is Zone 10.
June 18, 2021
바카라사이트 Keep up the good work you are doing here,it's very helpful my friend.
June 18, 2021
I bookmark this site and will find your posts frequently in the future.온라인바둑이
June 15, 2021
This information really helps me. It was actually a nice and useful piece of information. 메리트카지노
June 12, 2021
We are really grateful for your blog post for giving a lot of information 카지노사이트
March 29, 2021
Great post, very informative. I wonder why the other experts of this sector do not realize this. You should continue your writing. I am sure, you have a huge readers’ base already! 배트맨토토
February 16, 2021
Thank you for your great writing. Please continue to write good things. I'll bookmark it and visit often. P2P 사이트 순위
January 6, 2021
Hello I am an umble person from Portugal(europe). I´m navigate in Internet looking for Abandonnated churches, cemeteries, old monuments (castles,hotels,factories,etc.) I like to see. (I fill sad.) Manuel Mota mota@jardicentro.pt
November 27, 2020
What's up colleagues, nice article and nice urging commented at this place, I am truly enjoying by these.
November 9, 2020
Hi Mia, the Duval County Extension office should be able to help you with that question. Dr. Kerr is the commercial horticulture agent there, his email is CKERR@COJ.NET. Thanks for reading!
November 9, 2020
Awesome Frank, will do! Thanks so much for the suggestion. :)
November 9, 2020
Please, please, please add the FL native climbing aster! (Symphyotrichum carolinianum) The incredible explosion of fragrant purple flowers arrives in November & December, at a point when many other FL wildflowers are fading. To me, the flowers smell like sweet, warm sugar cookies! It's always loaded with pollinators too... Perfect for wetter soils - along the edges of ponds, swales, etc. Thanks, Frank Galdo - Program Coordinator, Florida-Friendly Landscaping, UF/IFAS Extension Pasco County Pics & info: https://flawildflowers.org/flower-friday-symphyotrichum-carolinianum/ http://hawthornhillwildflowers.blogspot.com/2009/11/climbing-aster-symphyotrichum.html https://twitter.com/PascoExt/status/1243217796705763329
June 28, 2020
These plants are very hard to find for purchase. Do you know anywhere in the Jax area? Thank you
June 11, 2020
It as hard to find experienced people in this particular topic, however, you sound like you know what you are talking about! Thanks
May 13, 2020
Thanks and you're welcome! - gus
May 13, 2020
Thanks for your comments! There are so many math and physics principles practiced and demonstrated in archery! If an instructor can remember to point them out while the kids are on the range, he or she can really reinforce what is taught in the classroom. All the instructor has to do, is find the appropriate teachable moment and take advantage of it. gus
May 8, 2020
This is a great use of math an angles to help improve your archery shooting range. When teaching a beginner having them line up a 90 degree angle will be helpful for them to take the same stance each time. Thank you
May 6, 2020
Informative, Thanks for this.
April 30, 2020
Thanks for your comments! I feel the same way. - gus
April 30, 2020
fishing is a awesome hobbit. I want fishing again and again.
March 26, 2020
Hey Steven! Thanks for your comment. I suggest you get into hunting with a multi-tiered approach, making sure you are comfortable in the woods, you know the laws and regulations of what you plan on hunting, and starting small - with small game that is. Hunting, which includes dispatching small game takes the same skills as hunting large game but with less input and intensity. If you can successfully bag your first raccoon (for example) and process it all the way to the table, you'll be well on your way to hunting larger game as you gain experience. If you haven't taken it, or done it lately, enroll in your local Hunter Safety class by your state game division. They can help. Go out into the woods and scout around. Go to the range and perfect your skills. All these things will not only prepare you for hunting, but will help you decide IF and how you want to go ahead. I hope that helps! - gus
March 25, 2020
Great share. I am new in hunting. Should I start with deer hunting? What your recommandation?
July 8, 2019
I'm glad you enjoyed the article! gus
June 19, 2019
Great to hear Joe! Send me a picture of it. gkoerner@ufl.edu I'd love to see it! gus
May 12, 2019
Haha I did it I made awing bone call . Thanks for the information .
March 6, 2019
Thank you for your nice blog post. Keep it up.
March 5, 2019
Thank you very much, Gary! I have been impressed with the BMP efforts of the Brevard turf professionals I've visited and will most definitely be helping with the implementation of new programs and certifications in environmental stewardship. Stay tuned!
March 5, 2019
Thank you for your post. Keep it up.
March 4, 2019
This is a great article Bonnie. Thank you very much for taking the time to visit the courses and talk to the superintendents. I am sure that you were pleased with the knowledge and effort they use daily to be stewards of the environment. Many are BMP Certified but we need more to get this certification and implement new programs to make the best agronomic and environmental decisions on a daily basis.
February 18, 2019
The counties currently involved in the FL Horseshoe Crab Watch Program are Franklin, Taylor, Dixie, Levy, Hernando, Pinellas, Manatee, Martin, Indian River, Brevard, Volusia, and Nassau. There are some counties that will be incorporated in the future including those in Southwest Florida (and Collier county). Here on the East Coast of Florida we see horseshoe crabs nesting between December-May depending on where you are. On the Gulf Coast of Florida they see them nesting in the spring and fall (Feb-May and Aug-Oct). It's unknown what the nesting time is in southwest Florida. If you ever do see horseshoe crabs please report them to the FWC Wildlife Hotline for horseshoe crabs at this link: https://myfwc.com/research/saltwater/crustaceans/horseshoe-crabs/ (click on Report Your Nesting Horseshoe Crab Sighting). You can also download the free FWC Reporter App and report sightings through your mobile device (https://myfwc.com/news/all-news/sighting-app/).
February 17, 2019
Is any yagging being done in Collier County? When is the best timr of yr to watch for mating crabs? Several yrs ago I was doing daily searches at Tigertail beach/lagoon. Found a good number that I sexed, measured etc. Never knrw where to send tbe data. Any contact person for this area?
December 3, 2018
Thanks Michael. I've put you down on my list and will be in touch once training dates are set.
December 3, 2018
Thanks Ivan. I've put you down on my list and will be in touch once training dates are set.
November 29, 2018
Hi Erin, unfortunately I do not have another one planned. I will keep your email address and let you know if we have another one.
November 29, 2018
Hi Cynthia, this class was in August. I don't have another one planned.
November 26, 2018
I'm in for a mid Brevard county location.
November 14, 2018
Would you please provide me with more information, like date and cost?
November 13, 2018
I'm interested and can work for Kirk in Indian River County or Holly in mid to south Brevard.
November 5, 2018
thank you for the info, very interesting
October 17, 2018
Is this going to be offered anytime soon? I was registered for a previous course but it was cancelled. Thank you. Erin
October 11, 2018
Thank you Mary. Feel free to call me anytime to discuss youth shooting sports in our region. Gus 321-633-1702, Ext. 52320
September 27, 2018
Gus, We shoot lever action smallbore and pistol cartridge rifle metallic silhouette at Seminole County Gun and archery and Chuluota Sportsmans Club on second Saturday and second Sunday of each month. Also smallbore and Hunters Pistol at Chuluota SC. Mary Watkins
June 14, 2018
We have just posted an article about the Tegu Lizard being spotted in Brevard County.
May 22, 2018
Thanks Mr. Gus!
Comments are closed.