By Simona Picardi, PhD student, Wildlife Ecology & Conservation Dept.

Incorporating cutting-edge mathematical tools in macroecological theory, in order to gain better understanding of large ecological systems’ function: this is the challenge undertaken by Dr. Stefano Allesina and his research team. After earning his PhD in Italy at the University of Parma, Dr. Allesina traveled to the US to complete three post-docs at Michigan State University, University of Michigan and University of California, Santa Barbara. He is now a Professor at the Department of Ecology & Evolution and Computation Institute at the University of Chicago. Dr. Allesina leads an incredibly productive research lab, boasting an impressive list of publications in journals the likes of Nature, PLoS One, Ecology, Ecology Letters, Trends in Ecology and Evolution, and more.

When Dr. Allesina speaks, you can sense the analytical rigor of the brilliant mathematician combined with a theoretical ecologist’s love of complexity. All that spiced up with a pinch of Italian humor. No wonder he is already so successful at such a young age.

Dr. Allesina’s lab specializes in the development of new mathematical, statistical and computational methods for theoretical ecology as well as broader applications. The bulk of Allesina’s work is focused in macroecology. The domain his research team covers is extremely vast, but shares a common theme: discovering how different species interact in nature to form ecological networks and food webs, how they react to extinctions, and how stability is reached in large systems. Another branch of the lab’s activity focuses on the science of science ­– methods for evaluating the impact of researchers, and refining peer-review algorithms in order to make science more sound and impactful.

Random Matrix Theory (henceforth, RMT) is the field of mathematics devoted to the study of large matrices whose coefficients are randomly sampled from specific distributions. RMT methods are borrowed from physics, where they were introduced in the fifties, before experiencing a huge proliferation and becoming one of the fastest growing areas of mathematics. According to Dr. Allesina, they are a fundamental mathematical tool needed to study the properties of large ecological systems. RMT is particularly suited for ecological systems, as it accounts for three very important characteristics of ecological systems: they are large, network-structured, and variable.

The study of equilibrium in large ecological systems has its roots in the work of Robert May (May, 1972), who demonstrated how to predict the stability of an equilibrium by analyzing the properties of the corresponding community matrix (i.e. a matrix describing all the interactions between populations in the community). If all the eigenvalues of the matrix have negative real parts the equilibrium is stable, whereas if any of them have positive real parts, the equilibrium is unstable.

May showed that, in order to make the probability that all the eigenvalues have negative real parts very high, a community matrix cannot be too large, or too connected, or with a large variance of the interactions. This discovery set into motion the “stability-complexity” debate among ecologists, which still remains unresolved.

Forty years of silence followed May’s work, and Allesina and his collaborators have been the first to get back to it. In order to extend May’s work with simple random matrices to more complex cases Dr. Allesina and his lab members applied three mathematical laws.

First, the semicircle law, named after the physicist Eugene Wigner, states that the limiting distribution of eigenvalues that arises for a random symmetric matrix as its size approaches infinity takes the form of a semicircular distribution centered at (0,0) in the plan described by a real horizontal axis and a vertical imaginary axis.

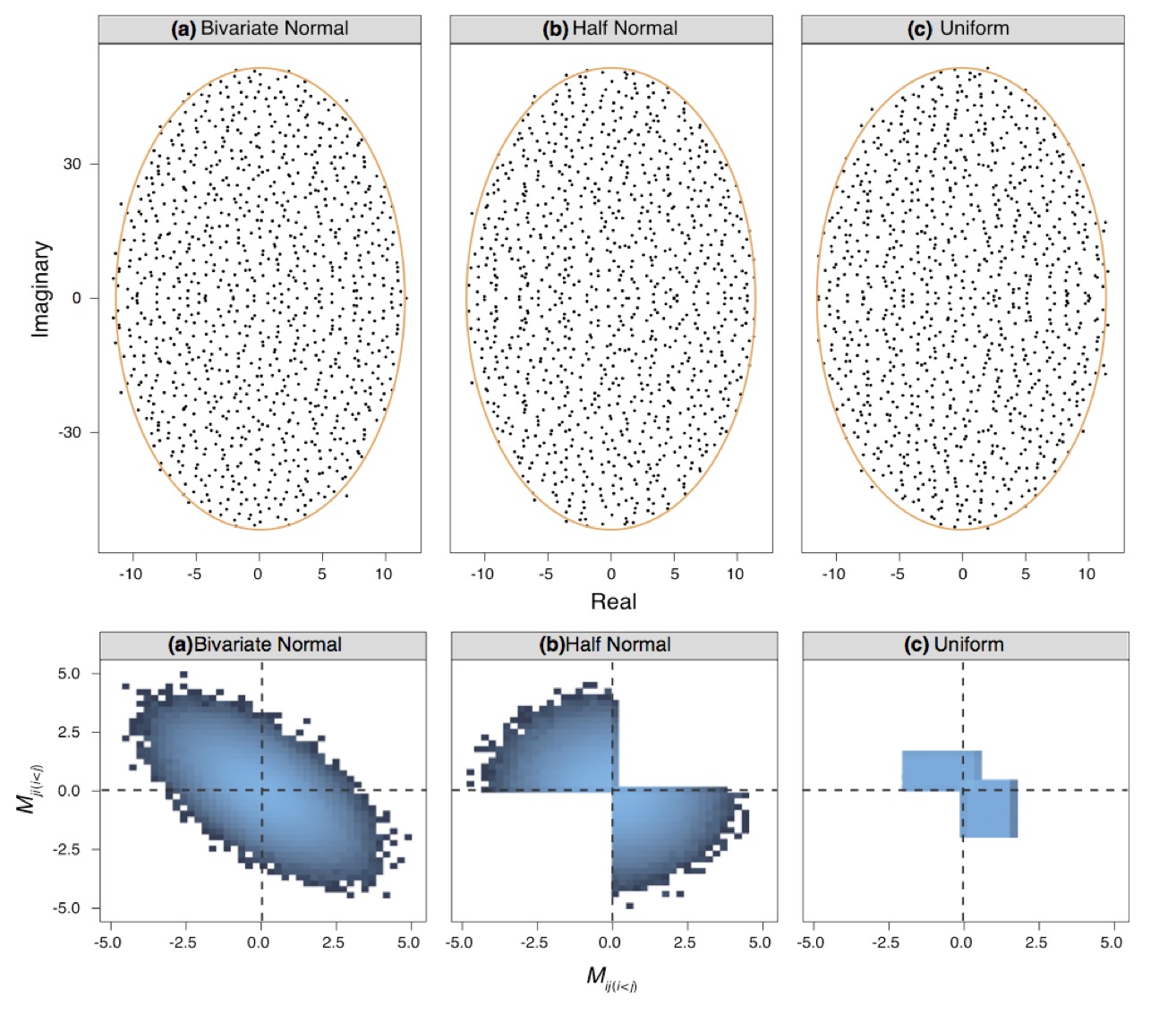
Second, the analog of Wigner’s semicircle law in the case of non-symmetric matrices is known as the circular law. The limiting distribution of eigenvalues for matrices whose size approaches infinity, in the case of asymmetry, is a circle centered at (0,0) and with radius √S. This law holds true regardless of the distribution from which matrix coefficients are drawn. This property is called universality, which Allesina refers to as “excellent news for ecology,” because the distribution of coefficients of a community matrix is seldom known.

In ecological networks, most of the time we deal with interactions where the fate of species are linked to each other, such as consumer-resource, mutualism, or competition. In such cases, we want to sample the matrix coefficient in pairs, rather than each coefficient separately. Doing so leads to the elliptic law, a generalization of the circular law in which the paired coefficients are drawn from a bivariate distribution. According to the elliptic law, the limiting distribution of the eigenvalues for a matrix with paired coefficients is an ellipse centered at (0,0).

The circular and elliptic law can both be extended to more general cases in order to account for partially connected matrices, diagonal elements that differ from zero, off-diagonal coefficients sampled from a bivariate distribution with non-zero marginal means, and more. Such modifications allow the mathematical model to follow the reality of ecological systems more closely, so that we can draw more realistic conclusions about them.

According to Dr. Allesina, there are a few main challenges that the scientific community will face in the next few years with respect to RMT applications in order to improve our understanding of stability in large systems.

First, since most of real ecological systems are governed by out-of-equilibrium dynamics, we need to find ways to predict the persistence of large ecological systems under non-equilibrium conditions. This will involve exploring the applicability of the methods developed for local stability to a wider domain. Being able to do so would have a strong impact on our understanding of what determines persistence in ecological systems.

Second, we need to include the distribution of species abundance in the models of stability, to account for the effect of the distribution shape on the stability of ecological communities. Solving this question could build a bridge connecting two huge ecological problems – stability and species abundance distributions – that are now quite separate, and could cast some light on possible causality relationships between these two phenomena.

Third, we have to overcome the constraint of the matrix representing a random network, simply because, as Dr. Allesina puts it in one of his most recent papers, the lion can’t be as likely to eat the gazelle as the gazelle is to eat the lion. Real food webs are anything but random. Instead, they are organized in modules, and there must be a ceiling threshold for the values of connectance (even hypothesizing a worldwide food web, the number of possible trophic connections for a single species would level off at some point).

Each of these challenges has the ultimate goal to bring more and more biological realism into analytical matrices. Dr. Allesina declares himself hopeful that most of these advancements can be achieved by the time May’s paper turns fifty years old. For that, we can count on Allesina’s work in the years to come.

0